A - Poisonous Cookies
题意
有若干饼干,分别是 \(A\) 块带有解毒剂的不好吃的饼干、\(B\) 块带有解毒剂的好吃的饼干、\(C\) 块带有毒药的好吃的饼干。
你可以按任意顺序吃任意数量的饼干,但是需要满足不能连续吃两块带有毒药的饼干。
求最多能吃多少块好吃的饼干。
\(A,B,C\le 10^9\)
题解
带有解毒剂的饼干一定全部都吃,这样带有毒药的饼干最多可以吃 \(A+B+1\) 块。
所以答案即为 \(B+\min(C,A+B+1)\)。
B - Tree Burning
题意
有一个周长为 \(L\) 的圆,你的起点在圆周上的某一位置,圆上的每个位置的坐标定义为从起点逆时针走到该点的距离,坐标范围为 \([0,L)\)。
有 \(N\) 棵树,第 \(i\) 棵树在坐标 \(x_i\)。你需要从起点出发,每次向左或向右走到第一棵树烧掉,直到树都被烧完。
求走的路程的最大值。
\(N\le 2\times 10^5,L\le 10^9\)
题解
我们把 \(N\) 棵树的坐标放在数轴上,那么数轴上 \([0,L)\) 的区间被分成了 \(N+1\) 段。
考虑每一段的贡献,一定是存在一个分界点 \(p\),\(p\) 前面部分是从前往后若干段连续递减到 \(0\) 的偶数,后面部分是从后往前连续递减到 \(1\) 的奇数,或者相反。同时需要保证第一段和最后一段的贡献差的绝对值为 \(1\)。
若前面部分和后面部分同时存在贡献相同的长度超过 \(1\) 的段,那么可以通过调整使得贡献更大,例如:
\[\{5,3,3,3,1,0,2,4,4\}\to\{7,5,3,3,1,0,2,4,6\}\]
并且如果存在这样的段,一定是贡献最大的段,否则也可以调整:
\[\{7,5,3,3,1,0,2,4,6\}\to\{7,7,5,3,1,0,2,4,6\}\]
于是枚举分界点后贡献就确定了,预处理 \((x_i-x_{i-1})\times i\) 的前缀和即可。
时间复杂度 \(O(N)\)。
C - Coloring Torus
题意
给定正整数 \(K\),你需要选择一个 \(1\) 到 \(500\) 的整数 \(n\),并构造一个 \(n\times n\) 的网格,记行列标号分别为 \(0,\ldots,n-1\),满足:
- 每个格子为 \(K\) 种颜色之一且每种颜色都至少出现一次。
- 对于两种颜色 \(i,j\),对于所有颜色为 \(i\) 的格子,与该格子相邻的颜色为 \(j\) 的格子数量相等。在这里,与 \((r,c)\) 相邻的格子为 \(((r-1)\bmod n, c), ((r+1)\bmod n, c), (r, (c-1)\bmod n), (r, (c+1)\bmod n)\)。
\(1\le K\le 1000\)
题解
先考虑 \(n\) 为偶数且 \(K=2n\) 的情况。有一种方案是将每行交替填上两种颜色,但是这样填并不能扩展。
考虑斜着填,对于所有 \((i-j)\bmod n\) 相同的位置,按 \(i\) 从小到大的顺序交替填上两种颜色。
这样构造显然是正确的。
另外,若我们将某一斜线填上同种颜色,这样的方案仍然是正确的的,这样我们就可以将颜色数减小。
于是取 \(n=2\lceil\frac{K}{4}\rceil\) 后按上述方法构造即可。
D - Inversion Sum
题意
有一个序列 \(A_1,A_2,\ldots,A_N\),有 \(Q\) 次操作,第 \(i\) 次操作你可以交换 \(A_{X_i}\) 和 \(A_{Y_i}\) 或者什么都不干。
求所有 \(2^Q\) 个最终序列的逆序对之和,对 \(10^9+7\) 取模。
\(N,Q\le 3000\)
题解
考虑对于每一对数计算贡献。
考虑 DP,令 \(f_{k,i,j}\) 表示从第 \(k\) 次操作开始,当前位置分别为 \(i\) 和 \(j\) 的两个数,在最终序列中第一个数在第二个数前面的方案数。
转移很简单,注意到除了第 \(X_k,Y_k\) 行和第 \(X_k,Y_k\) 列外,其他位置的 DP 值的操作只是乘了 \(2\)。
于是我们只需要记录当前 DP 数组实际需要乘上的值,每次就可以 \(O(N)\) 转移。
这本质上与方案数转概率相同。
时间复杂度 \(O(N(Q+N))\)。
E - Less than 3
题意
若一个 \(01\) 字符串中不存在连续 \(3\) 个 \(0\) 或连续 \(3\) 个 \(1\),那么称之为好的。
有两个长度为 \(N\) 的好的 01 字符串 \(s,t\)。你可以对 \(s\) 执行若干次以下操作:
- 选择一个位置取反,需要保证操作后字符串仍然是好的。
求使得 \(s\) 变为 \(t\) 的最少操作次数。
\(N\le 5000\)
题解
考虑在相邻的 \(01\) 之间放一条红线,相邻的 \(10\) 之间放一条蓝线,并且前后交替放置无限条红线和蓝线。
那么一次操作相当于把一条线向左或向右移动一格。除了首尾,需要保证每个位置最多只有一条线,且相邻的线距离最多为 \(2\)。一个操作过程的例子如下图所示(来自官方题解):
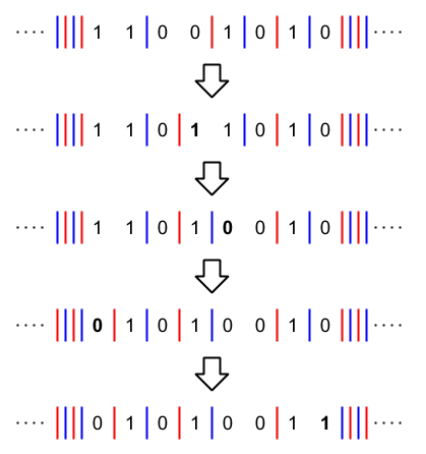
若我们得到了 \(s\) 和 \(t\) 线与线的对应关系,可以证明一定有解,且答案即为每一个对应关系中两条线的距离之和。一个例子如下图所示(来自官方题解):
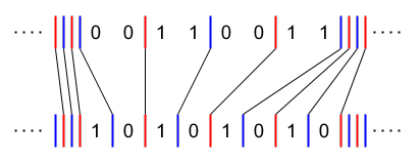
该例子的答案为 \(\cdots+0+0+0+1+0+1+2+3+2+1+0+\cdots=10\)。
对应关系只有 \(O(N)\) 种,枚举即可。
时间复杂度 \(O(N^2)\)。
F - Permutation and Minimum
题意
给定一个未填完的 \(1\) 到 \(2N\) 的排列 \(A_1,A_2,\ldots,A_{2N}\),你需要填完该排列,然后得到一个新的序列 \(B_1,B_2,\ldots,B_N\),其中 \(B_i=\min(A_{2i-1},A_{2i})\)。
求可以得到多少不同的序列 \(B\)。对 \(10^9+7\) 取模。
\(N\le 300\)
题解
咕咕咕



