A - Limited Insertion
题意
有一个初始为空的序列 \(a\)。
你需要执行 \(N\) 次操作,第 \(i\) 次操作需要选择一个 \(j\ (1\le j\le i)\),在 \(a\) 中的位置 \(j\) 插入 \(j\)(序列最开始为位置 \(1\))。
给定一个长度为 \(N\) 的序列 \(b\),构造一种操作序列使得最后 \(a=b\),或输出无解。
\(N\le 100\)
题解
显然若存在 \(a_i > i\) 一定无解,否则可以通过构造证明一定有解。
考虑倒着做,每次找到最后一个 \(a_i=i\) 的位置删除,这样可以使得该序列仍然满足 \(a_i\le i\)。
时间复杂度 \(O(N^2)\)。
B - Balanced Neighbors
题意
构造一个 \(N\) 个点的简单无向连通图 \(G\),满足存在一个 \(S\),使得对于所有 \(1\le i\le N\),与 \(i\) 相连的节点编号之和等于 \(S\)。
\(N\le 100\)
题解
我们可以首先构造一个完全图,发现此时与 \(i\) 相连的节点编号之和为 \(\frac{n(n+1)}{2}-i\)。
考虑去掉所有形如 \((i,n-i)\) 的边,那么与 \(i\) 相连的节点编号之和为 \(\frac{n(n+1)}{2}-i-(n-i)=\frac{n(n+1)}{2}-n\),是一个定值。
但是这样构造在 \(n\) 为偶数时会有问题,于是当 \(n\) 是偶数时我们去掉所有形如 \((i,n+1-i)\) 的边即可。
C - Three Circuits
题意
给定一个 \(N\) 个点 \(M\) 条边的简单无向连通图 \(G\),判断是否可以在 \(G\) 中找出三个环使得每条边恰好被一个环覆盖。
这里的环是指每条边只能经过一次但点可以经过多次的环。
\(N,M\le 10^5\)
题解
显然若存在度数为奇数的点一定不合法。
当存在度数大于 \(4\) 的点时,设该点为 \(x\),考虑从 \(x\) 开始的一条欧拉回路,记录每次访问的节点编号,我们可以每次将两个 \(x\) 之间的部分作为一个环删去,可以至少删三次,所以一定有解。
当度数等于 \(4\) 的点数小于 \(2\) 时,那么一定不合法。
当度数等于 \(4\) 的点数等于 \(2\) 时,设这两个点为 \(x,y\),若我们把度为 \(2\) 的点组成的链缩成一条边,那么要有解必须是 \(x\) 和 \(y\) 有两条边且 \(x\) 和 \(y\) 各自有一个自环的形式。可以简单判断。
当度数等于 \(4\) 的点数大于 \(2\) 时,根据类似于存在度数大于 \(4\) 点时的分析,我们可以从一个度数等于 \(4\) 的点 \(A\) 开始分成两个环。这两个环一定是以下两种情况之一(图来自官方题解):
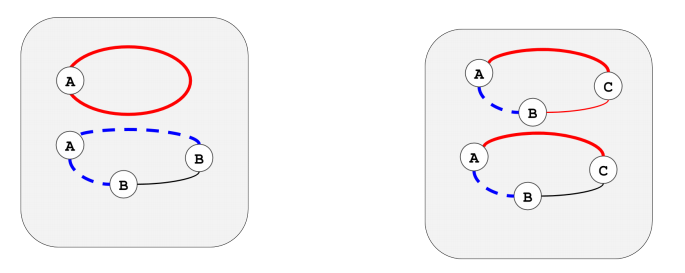
可以发现这两种情况都可以构造出三个环。于是这种情况也一定有解。
D - Rotation Sort
题意
给定一个 \(1\) 到 \(N\) 排列 \(p\),你可以执行若干次以下操作:
- 花费 \(A\) 的代价,将一个区间循环左移一格;
- 花费 \(B\) 的代价,将一个区间循环右移一格。
求使得排列 \(p\) 有序的最小代价。
\(N\le 5000\)
题解
可以发现循环左移相当于将一个数插入到后面,循环右移相当于将一个数插入到前面。
那么没有被操作的数一定是一个上升子序列 \(x_1 < x_2 < \ldots < x_k\ (p_{x_1} < p_{x_2} < \ldots < p_{x_k})\),而对于 \(x_{i-1}\) 到 \(x_i\) 之间被操作的位置 \(j\),若 \(p_j > p_{x_i}\),则需要花费 \(A\) 的代价,否则需要花费 \(B\) 的代价。
于是直接 \(O(N^2)\) DP 即可。可以用线段树优化到 \(O(N\log N)\)。
E - Modulo Pairing
题意
给定 \(2N\) 个整数 \(a_1,a_2,\ldots,a_{2N}\),以及一个整数 \(M\)。
我们需要将这 \(2N\) 个数划分成 \(N\) 个二元组,使得每个数恰好在一个二元组中出现。
一个二元组 \((x,y)\) 的权值为 \((x+y)\bmod M\),求 \(N\) 个二元组权值最大值的最小值。
\(N\le 10^5\)
题解
考虑对于一个二元组 \((x,y)\),若 \(x+y < M\),我们则将 \(x,y\) 和这条匹配边染成蓝色,否则染成红色。
将 \(a\) 从小到大排序,那么最后的匹配一定形如下图:
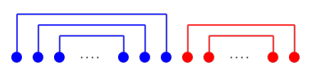
否则可以通过以下方式进行调整:
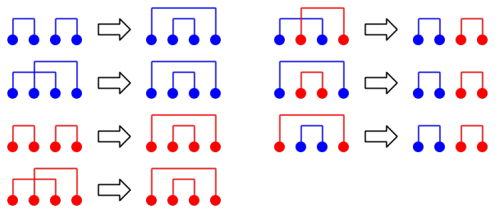
我们发现合法的分界点一定是一个区间,且越靠左越优。
于是二分答案即可。
F - One Third
题意
在一个圆上沿半径等概率随机切 \(N\) 刀,选择连续若干块,假设占整个圆面积的 \(x\) 倍,求 \(|x-\frac{1}{3}|\) 的最小值的期望。
\(N\le 10^6\)
题解
考虑将每一刀切的半径标红,并对于每一条标红的半径,分别将该半径绕圆心逆时针 \(120^{\circ}\) 和顺时针 \(120^{\circ}\) 处的半径标成蓝色和绿色,那么 \(|x-\frac{1}{3}|\) 的最小值等于两条不同颜色的半径形成的夹角与 \(360^{\circ}\) 的比值的最小值。
注意到这个最小值一定会取在相邻的两条不同颜色半径上。
我们将第一刀对应的半径记为 \(0^{\circ}\),我们可以只保留 \(0^{\circ}\) 到 \(120^{\circ}\) 之间的半径,\(120^{\circ}\) 到 \(240^{\circ}\) 之间和 \(240^{\circ}\) 到 \(360^{\circ}\) 之间与这一部分等价,不需要考虑。
于是问题转化成:在一个数轴上,一开始在 \(0\) 和 \(\frac{1}{3}\) 处分别有一个红点和蓝点。然后在 \([0,\frac{1}{3}]\) 中随机放置 \(N-1\) 个随机颜色(红、蓝、绿)的点。求异色点距离最小值的期望。
我们可以求出 \(f(k)\) 表示有恰好 \(k\) 对相邻异色点的概率,\(g(k)\) 表示有恰好 \(k\) 对相邻异色点时异色点距离最小值的期望,那么最后答案为 \(f(k)g(k)\) 之和。
\(f(k)\) 可以通过 DP 或组合数计算。\(g(k)\) 可以考虑 \(k\) 对相邻异或点距离的总和为 \(\frac{k}{3n}\),而将一条线段随机分成 \(k\) 段,最小的一段的期望长度为总长的 \(\frac{1}{k^2}\),所以 \(g(k)=\frac{1}{3nk}\)。 后面部分的具体计算过程可以参考曾加的回答 - 知乎。



