A - XOR Circle
题意
给定 \(N\) 个非负整数 \(a_1,a_2,\ldots,a_N\),判断是否可以将这 \(N\) 个数放入一个环中,使得每个数左右两边数的异或值等于该数。
\(N\le 10^5,a_i\le 10^9\)
题解
条件相当于连续三个数异或和等于 \(0\)。假设最后环上的数按顺序为 \(b_0,b_1,\ldots,b_{n-1}\),那么一个必要条件是 \(b_i=b_{(i+3)\bmod n}\)。
当 \(3\nmid n\) 时,该条件相当于所有数相等。又因为需要连续三个数异或和为 \(0\),那么所有数必须都是 \(0\)。
当 \(3\mid n\) 时,我们需要将所有数分成 \(3\) 组,每组有 \(\frac{n}{3}\) 个数且都相等。同时为了满足连续三个数异或和为 \(0\),这三组中各取一个数的异或和需要等于 \(0\)。直接判断即可。
时间复杂度 \(O(n)\) 或 \(O(n\log n)\)。
B - Even Degrees
题意
有一张 \(N\) 个点 \(M\) 条边的简单无向连通图,你需要给每条边定向,使得每个点的出度为偶数。构造一组方案,或输出无解。
\(N,M\le 10^5\)
题解
当 \(M\) 是奇数时一定无解,\(M\) 是偶数时可以通过构造证明一定有解。
当图是一棵树时,我们只需要从叶子向上依次确定边的方向即可。
对于原问题,我们只需要任意取出一棵生成树,任意确定非树边的方向,再用类似树的方法确定树边的方向即可。
时间复杂度 \(O(N+M)\)。
C - Skolem XOR Tree
题意
有 \(2N\) 个点,第 \(i\ (1\le i\le N)\) 个点和第 \(N+i\) 个点的点权为 \(i\)。
将这 \(2N\) 个点连成一棵树,使得:
- 对于所有 \(1\le i\le N\),\(i\) 和 \(i+N\) 路径上点权的异或和为 \(i\)(包括两个端点)。
\(N\le 10^5\)
题解
当 \(N=2^k\) 时一定无解,因为除去 \(N\) 和 \(2N\) 两个点其他点权最高位都小于 \(k\),不可能使得异或和为 \(2^k\)。
注意到 \(2i\) 和 \(2i+1\) 的异或值为 \(1\)。当 \(N\) 是奇数时,我们可以以节点 \(1\) 为中心构造一条链,每次将点权为 \(2i\) 和 \(2i+1\) 的点对分别放在两边。例如 \(N=5\) 时我们可以构造 \[4-5-2-3-1-2-3-4-5\]
然后将另一个点权为 \(1\) 的点连在第一对点对上即可,例如上面的例子中连在右边的 \(3\) 上即可。
当 \(N\) 是偶数时,我们一定可以找到一个 \(x,y\ (2\le x,y < N)\) 使得 \(N=x\oplus y\)。那么我们只要强制链的一边 \(x,y\) 有连边即可,例如 \(N=6,x=2,y=4\) 时,可以构造 \[4-5-3-2-1-3-2-4-5\]
然后将两个 \(6\) 分别连在右边的 \(2\) 和 \(4\) 上即可。
D - Add and Remove
题意
有 \(N\) 张卡片,从左到右分别写着数字 \(A_1,A_2,\ldots,A_N\)。执行以下操作若干次直到卡片数量为 \(2\):
- 选择连续三张卡片 \(x,y,z\);
- 将 \(A_x\) 和 \(A_z\) 各加上 \(A_y\),然后删去第 \(y\) 张卡片。
求最后两张卡片上的数字之和的最小值。
\(N\le 18\)
题解
考虑倒着做,令 \(f_{l,r,x,y}\) 表示只考虑 \([l,r]\) 中的卡片,其中 \(l\) 最后会对答案产生 \(x\) 倍的贡献,\(r\) 最后会对答案产生 \(y\) 倍的贡献时的最小值(不计入卡片 \(l,r\) 上原来的数的贡献)。那么有 \[ f_{l,r,x,y}=\min_{l < k < r} f_{l,k,x,x+y}+f_{k,r,x+y,y}+A_k(x+y) \]
可以证明状态数为 \(O(2^n\operatorname{poly}(n))\)。
时间复杂度 \(O(2^n\operatorname{poly}(n))\)。
E - Develop
题意
有一个集合 \(S\),初始为所有整数。每次可以执行以下操作:
- 选择一个 \(1\) 到 \(N\) 且在 \(S\) 中的整数 \(x\),在 \(S\) 中删除 \(x\);
- 在 \(S\) 中加入 \(x-2\) 和 \(x+K\)。已经存在则不加入。
求通过若干次(可以是 \(0\) 次)操作可以得到的不同的集合数量。对 \(M\) 取模。
\(N\le 150\)
题解
考虑 \(x\) 向 \(x-2\) 和 \(x+K\) 连有向边。我们可以将最终集合的数量转化为删去的数组成的集合的数量。显然一个环中的数不能都被删去,而删去的数构成的子图若不存在环那么一定合法。
当 \(K\) 为偶数时,图的形态如下图所示(图中 \(N=11,K=6\)):
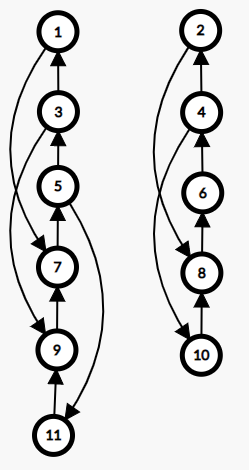
这相当于对于每一条链,不能连续选择超过 \(\frac{K}{2}\) 个点,对每条链分别 DP 即可。
当 \(K\) 为奇数时,图的形态如下图所示(图中 \(N=12,K=3\)):
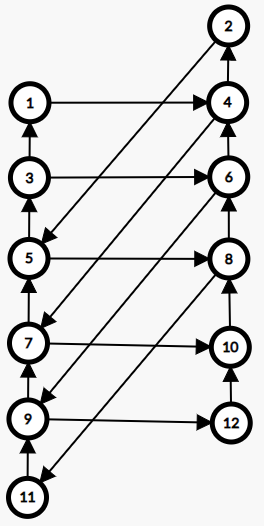
图中的一个环一定是从左边的某个点向上,到某个点往右,然后再往上,最后回到原点。即在上图中形如一个三角形或一个八字形。
注意图中的每个简单环长度都为 \(K+2\),那么相当于不能存在一条向上、向右、再向上的,长度为 \(K+2\) 的路径。
于是可以 DP,令 \(f_{i,j,k}\) 表示到图中的第 \(i\) 层,从第 \(i\) 层左侧点开始的向上、向右、再向上的最长的路径长度为 \(j\),从右侧点向上的最长路径长度为 \(k\) 时的方案数。
注意当上一层的 \(j\) 为 \(0\) 且这一层右侧点没有选择时,这一层的 \(j\) 仍然是 \(0\),因为要形成环必须要有一条向右的边。
时间复杂度 \(O(N^3)\)。
F - Two Histograms
题意
有一个 \(N\times M\) 的网格,初始都为 \(0\)。你需要执行一次以下操作:
- 对于每个 \(1\le i\le N\),选择一个 \(0\le k_i\le M\),将第 \(i\) 行的前 \(k_i\) 个格子中的数加 \(1\)。
- 对于每个 \(1\le j\le M\),选择一个 \(0\le l_j\le N\),将第 \(i\) 列的前 \(l_j\) 个格子中的数加 \(1\)。
求最后能得到多少本质不同的网格。对 \(998244353\) 取模。
\(N,M\le 5\times 10^5\)
题解
注意到对于一个 \(\{k_i\},\{l_j\}\),若存在 \(i,j\) 满足 \(k_i=j-1,l_j=i\),那么我们可以把 \(k_i\) 加 \(1\),\(l_j\) 减 \(1\) 而不改变矩阵。由于每次改变会使 \(k\) 的总和增加,所以改变次数一定是有限的。我们称不存在这样 \(i,j\) 的 \(\{k_i\},\{l_j\}\) 为标准形式。
接下来我们证明一个合法的网格一定对应唯一的一个标准形式。
假设一个网格对应两个不同的标准形式,分别为 \(\{k_i\},\{l_j\}\) 和 \(\{k_i'\},\{l_j'\}\)。令 \(j\) 为第一个满足 \(l_j\ne l_j'\) 的位置。
不妨假设 \(l_j < l_j'\)。若 \(j=1\),那么网格的第 \(l_1'\) 行第 \(1\) 列一定为 \(1\),所以有 \(k_{l_1'}'=0\),与 \(\{k_i'\},\{l_j'\}\) 是标准形式矛盾。
若 \(j>1\),那么网格的第 \(l_j'\) 行第 \(j\) 列一定为 \(1\),所以有 \(k_{l_j'}\ge j,k_{l_j'}' < j\)。又因为 \(k_{l_j'}'\ne j-1\),所以 \(k_{l_j'}' < j-1 < k_{l_j'}\),又因为 \(l_{j-1}=l_{j-1}'\),网格的第 \(l_j'\) 行第 \(j-1\) 列一定不同,矛盾。
于是接下来我们只要统计不存在 \(i,j\) 满足 \(k_i=j-1,l_j=i\) 的 \(\{k_i\},\{l_j\}\) 的序列数量。考虑容斥,强制若干对 \(i,j\) 满足该条件,容斥式子为 \[ \sum_{i=0}^{\min(n,m)}(-1)^i\binom{n}{i}\binom{m}{i}i!(m+1)^{n-i}(n+1)^{m-i} \]
直接计算即可。
时间复杂度 \(O(n)\)。



