A - Connection and Disconnection
题意
给定字符串 \(S\) 和一个整数 \(k\),令 \(T\) 为将 \(S\) 复制 \(k\) 份依次拼接得到的字符串。
求最少需要改变 \(T\) 中的几个字符使得 \(T\) 中任意两个相邻的字符不同。
\(|S|\le 100,k\le 10^9\)
题解
考虑 \(k=1\) 时如何求答案。设字符相同的连续段长度依次为 \(l_1,l_2,\ldots,l_m\),那么答案为 \(\sum\limits_{i=1}^{m} \lfloor\frac{l_i}{2}\rfloor\)。
\(k>1\) 时只要特殊处理一下首尾的两个连续段字符相同的情况。
时间复杂度 \(O(|S|)\)。
B - Graph Partition
题意
给定一个 \(n\) 个点 \(m\) 条边的简单无向连通图。
判断是否将图分成若干层,使得任意一条边连接的点在相邻两层(不能是同一层)。若可行,求最大层数。
\(n\le 200\)
题解
有解的充要条件是没有奇环。
我们钦定一个点 \(u\) 在第一层,那么剩下点的分层方式一定是按 BFS 树分。具体证明可以根据 BFS 树的性质进行证明。
时间复杂度 \(O(N^3)\)。
C - Division by Two with Something
题意
给定一个整数 \(n\) 以及一个 \(n\) 位二进制数 \(X\),求对于 \(0\le k\le X\),执行若干次(不为 \(0\) 次)以下操作第一次变回原来的 \(k\) 的操作之和:
- 若 \(k\) 是奇数,则减 \(1\) 后除以 \(2\);若 \(k\) 是偶数,则除以 \(2\) 后加 \(2^{n-1}\)。
对 \(998244353\) 取模。
\(n\le 2\times 10^5\)
题解
先不考虑 \(X\) 的限制。
执行题目中的一次操作相当于把最后一位取反后放到最前面。而执行不超过 \(n\) 次操作相当于把一段后缀取反后放到最前面。
即若把操作的数的二进制表示从高位到低位看成一个字符串 \(S\),我们要求最小的 \(p\) 使得 \(\operatorname{not}(S[n-p+1,n])+S[1,n-p]=S\)。注意到若操作次数大于 \(n\),条件与上述条件相同,所以若不存在这样的 \(p\) 那么答案一定是 \(2n\)。
发现满足上述条件的字符串一定是由一个长度为 \(d\ (d\mid n,d < n)\) 的字符串每次取反加入到 \(S\) 中,执行 \(\frac{n}{d}\) 次后得到的结果。如 \(n=9,d=3\) 时,可以构造出形如 \(000111000,001110001\) 的字符串。而这样构造得到的字符串一定有最小的 \(p=2d\)。
于是考虑枚举 \(d\),那么方案数为 \(2^d\),操作次数为 \(2d\),对答案的贡献为 \(2^d\times 2d\)。
可是这样做会有问题,例如 \(n=9,d=3\) 时会构造出 \(010101010\) 这样的字符串,但这样的字符串的 \(p\) 应为 \(2\),应该在 \(d=1\) 时被计算。所以容斥即可。
有 \(X\) 的限制时同理,前 \(d\) 位小于 \(X\) 的前 \(d\) 位时方案数就是 \(X\) 的前 \(d\) 位,等于时只有一种,直接构造出字符串判断是否小于等于 \(X\) 即可。
时间复杂度 \(O(d(n)n)\),其中 \(d(n)\) 表示 \(n\) 的因子数量。
D - Incenters
题意
给定单位圆上的 \(N\) 个点,求随机选择三个不同的点形成的三角形的内心的坐标的期望。
\(N\le 3000\)
题解
假设三角形的三个顶点为 \(A,B,C\),我们可以得到 \(\angle A,\angle B,\angle C\) 的角平分线与圆的交点,分别记做 \(A',B',C'\)。根据圆心角、圆周角的相关性质可以得到 \(A',B',C'\) 分别是弧 \(BC,CA,AB\) 的中点。可以根据这一性质继而证明 \(\triangle ABC\) 的内心与 \(\triangle A'B'C'\) 的垂心重合。
另外,根据欧拉线的相关性质,有三角形的重心 \(G\) 在外心 \(O\) 和垂心 \(H\) 的连线段上,且 \(OH=3OG\),即 \(\overrightarrow{OH}=3\overrightarrow{OG}\)。
于是我们把垂心的计算转化成了重心的计算。
三个点 \(A'(x_1,y_1),B'(x_2,y_2),C'(x_3,y_3)\) 形成的三角形的重心为 \((\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})\)。此题由于 \(A',B',C'\) 都在单位圆上,外心为原点,所以垂心即为 \((x_1+x_2+x_3,y_1+y_2+y_3)\)。
于是我们可以枚举 \(N\) 个点之间两两形成的弧,求出该弧的中点对答案的贡献即可。
时间复杂度 \(O(N^2)\)。
E - Pairing Points
题意
有 \(2N\) 个点共圆,按逆时针编号 \(1\) 到 \(2N\)。保证任意六个不同的点形成的三条线段不经过同一个点。
这些点之间有一些线段相连,你需要选出 \(N\) 条线段,使得:
- 每个点恰好属于一条选出线段。
- 若把选出的线段之间的交点看做顶点,把线段看做边,则形成一棵树。
求方案数。
\(N\le 20\)
题解
首先可以枚举与 \(1\) 相连的点,然后将环分成两部分。
令 \(f_{l_1,r_1,l_2,r_2}\) 表示 \([l_1,r_1]\) 与 \([l_2,r_2]\) 配对(中间已经有一条线段)的方案数。跨越中间的匹配一定是在 \([l_1,r_1]\) 中选一些点 \(x_1,x_2,\ldots,x_m\ (x_i < x_{i+1})\),在 \([l_2,r_2]\) 中选一些点 \(y_1,y_2,\ldots,y_m\ (y_i > y_{i+1})\),然后 \(x_i\) 与 \(y_i\) 匹配,如下图所示:
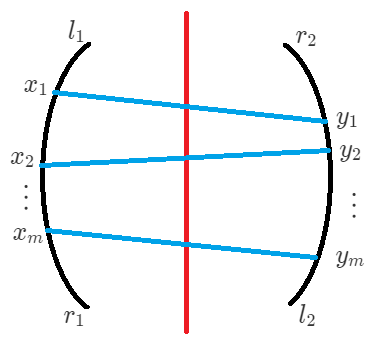
为了防止算重和方便转移,我们再引入 \(g_{l_1,r_1,l_2,r_2}\),定义与 \(f\) 类似,但是强制跨越中间的线段只能选一条。
那么 \(f\) 的转移只需要枚举 \(x_m,y_m\) 所在的区间即可:
\[f_{l_1,r_1,l_2,r_2}=\sum_{i,j} f_{l_1,i,j,r_1}\cdot g_{i+1,r_1,l_2,j-1}\]
\(g\) 的转移则只需要枚举匹配边即可:
\[g_{l_1,r_1,l_2,r_2}=\sum_{(i,j)\in E} f_{l_1,i-1,i+1,r_1}\cdot f_{l_2,j-1,j+1,r_2}\]
时间复杂度 \(O(N^6)\)。
F - Min Product Sum
题意
你需要在一个 \(N\times M\) 的网格的每个格子中填上 \(1\) 到 \(K\) 的一个整数。
定义一个格子的权值为所在的行和所在的列中元素最小值。
定义一个方案的权值为所有格子的权值的乘积。
求所有填数方案的权值之和,对给定的大质数 \(P\) 取模。
\(N,M,K\le 100\)。
题解
假设我们知道了每行的最小值 \(r_i\) 和每列的最小值 \(c_j\),则答案即为 \[\prod_{i=1}^{N}\prod_{j=1}^{M}\min(r_i,c_j)\]
而对于方案数,假设我们只考虑 \(a_{i,j}\ge r_i\) 和 \(a_{i,j}\ge c_j\) 的限制,则方案数为 \[\prod_{i=1}^{N}\prod_{j=1}^{M}(K-\max(r_i,c_j)+1)\]
为了强制取到最小值,只需要容斥即可,即强制一些行一些列大于钦定的最小值后计算即可。
于是我们可以 DP。令 \(f_{k,i,j}\) 表示填了 \(r_i,c_j\) 中小于等于 \(k\) 的值,且已经填的行数为 \(i\),列数为 \(j\) 时已填的位置对答案的贡献。
转移需要枚举加入的不被容斥的行数、不被容斥的列数、容斥的行数、容斥的列数,一起枚举复杂度过高,只要依次枚举,分四次转移即可。
时间复杂度 \(O(KNM(N+M))\),有点略微卡常。



