A - Integer Product
题意
给定 \(n\) 个小数点后最多 \(9\) 位的实数 \(A_1,A_2,A_3,\ldots,A_n\),求有多少对 \((i,j)\ (1\le i < j\le n)\) 满足 \(A_i\cdot A_j\) 为整数。
\(n\le 2\times 10^5,0<A_i<10^4\)
题解
令 \(a_i=10^9A_i=2^{x_i}5^{y_i}r_i\),将小数转化为整数。
则合法的 \((i,j)\) 需要满足 \(10^{18}|a_ia_j\),也就是满足 \(x_i+x_j\ge 18,y_i+y_j\ge 18\)。
直接枚举 \(x_i,x_j,y_i,y_j\) 即可。注意去掉 \(i\ge j\) 的情况。
记 \(m=\max\{a_i\}\),时间复杂度 \(O(n\log m+\log^4 m)\)。
B - First Second
题意
对于一个字符串,有一种操作是删除这个字符串的第一个字符或第二个字符。
有 \(n\) 个字符串 \(S_1,S_2,S_3,\ldots,S_n\),求有多少对 \((i,j)\ (1\le i < j\le n)\) 满足 \(S_i\) 和 \(S_j\) 中的其中一个字符串可以通过若干次上述操作得到另一个字符串。
\(n\le 2\times 10^5,\sum |S_i|\le 10^6,|\Sigma|\le 26,S_i\ne S_j\)。
题解
考虑两个字符串 \(A,B\ (|A|\le |B|)\) 可以从 \(B\) 变成 \(A\) 当且仅当 \(A[2..|A|]\) 是 \(B\) 的一个后缀,且 \(A[1]\) 在 \(B[1..|B|-|A|+1]\) 中出现。
将字符串翻转后,条件变为 \(A\) 可以拆成 \(B\) 中一个前缀加一个字符的形式。
考虑将所有 \(S_i\) 翻转后建 Trie,枚举每个字符串以及另一个字符串在该字符串中对应的前缀和后面加的字符即可。
时间复杂度 \(O(|\Sigma|\sum |S_i|)\)。
C - Product Modulo
题意
令质数 \(P=200003\)。给定 \(n\) 个整数 \(A_1,A_2,A_3,\ldots,A_n\),求 \[\sum_{i=1}^{n}\sum_{j=i+1}^{n} (A_iA_j\bmod P)\] 的值。
\(n\le 2\times 10^5\)
题解
求出 \(P\) 的一个原根 \(g=2\)。
于是我们可以将 \(A_i\) 表示成 \(g^{B_i}\bmod P\)。
于是 \(A_iA_j\bmod P=g^{B_i+B_j}\bmod P\)。
用 FFT 求出对于每个 \(k\) 求出 \(B_i+B_j=k\) 的 \((i,j)\) 数量即可。
时间复杂度 \(O(P\log P)\)。
D - Twin Binary Trees
题意
有两棵高度为 \(H\) 的满二叉树 \(T_1,T_2\),节点编号为从根开始逐层标号 \(1\) 到 \(2^H-1\)。
有一个 \(1\) 到 \(2^{H-1}\) 的排列 \(P\),表示 \(T_1\) 中编号为 \(2^{H-1}+i-1\) 的叶子与 \(T_2\) 中编号为 \(2^{H-1}+P_i-1\) 的叶子有一条特殊边。
定义一个环的权值为环上所有节点编号的乘积。
求所有恰好包含两条特殊边的简单环的权值之和。对 \(10^9+7\) 取模。
\(H\le 18\)
题解
一个暴力的想法是枚举 \(T_1\) 中的两个叶子 \(x,y\),然后能唯一确定一个简单环 \(x\to \operatorname{LCA}(T_1,x,y)\to y\to P_y\to \operatorname{LCA}(T_2,P_x,P_y)\to P_x\to x\)。
考虑枚举 \(x,y\) 在 \(T_1\) 上的 LCA \(u\),然后枚举 \(u\) 左子树中每个叶子 \(x\),在 \(T_2\) 中 \(P_x\) 到根路径上的每个点上加上对应的路径权值。
接下来枚举右子树中每个点 \(y\),枚举 \(T_2\) 中 \(P_y\) 到根路径上的每个点作为 \(P_x,P_y\) 的 LCA 计算贡献。
时间复杂度 \(O(2^H\times H^2)\)。
E - Product Simulation
题意
本题没有输入。
你可以在长度为 \(N=200000\) 的数组 \(a_0,a_1,a_2,\ldots,a_{N-1}\) 上执行以下两种操作:
- `+ i j k`,表示执行 \(a_k\gets a_i+a_j\)。\(i,j,k\) 不需要互不相同。
< i j k,表示执行 \(a_k\gets [a_i<a_j]\)。\(i,j,k\) 不需要互不相同。
初始时,\(a_0=A,a_1=B,a_2=a_3=\ldots=a_{N-1}=0\)。
你可以执行最多 \(Q=200000\) 次操作来实现 \(a_2\gets a_0\times a_1\)。
\(0\le A,B\le 10^9\)。注意你不知道 \(A,B\) 具体的值。
题解
首先考虑一个最简单的问题,实现 \(a_k\gets a_i\times a_j\),其中 \(a_i,a_j\in \{0,1\}\)。
在这种情况下,有一个简单的式子 \(a_i\times a_j=[1<a_i+a_j]\)。
假设我们已经在第 \(3\) 个位置构造出了 \(1\),则我们只要依次执行 + i j k 和 < 3 k k 即可。
注意到 \(A=B=0\) 时无论如何执行操作数组中都不可能出现除 \(0\) 以外的数,所以我们可以忽略这种情况。
在其他情况下,\(A<2(A+B)\) 恒成立,所以我们用该式子可以构造出 \(1\)。
构造出 \(1\) 以后,我们可以依次构造出 \(2^1,2^2,\ldots,2^{29}\)。
类似地,我们可以实现 \(a_x\gets a_x\times 2^k\) 的操作,只要执行 \(k\) 次 + x x x 即可。
接下来我们可以实现对非负整数 \(x\) 二进制分解。从高到低依次枚举 \(2^k\),用临时变量 \(S\) 存储已经确定的位,每次将 \(S+2^k<x+1\) 的值存在临时变量 \(t\) 中,将 \(t\) 的值赋值到存储分解结果的位置,然后将 \(t\) 乘上 \(2^k\) 后加到 \(S\) 中。可以发现这些操作都可以用上面讨论过的操作实现。
我们用上述操作将 \(A,B\) 分解后,枚举每一对二进制位 \((i,j)\),用之前提到过的 01 乘法和自乘 \(2\) 的幂次的操作即可实现乘法。
数组使用约 \(100\) 个,操作次数约为 \(30000\) 次。
F - Rooks
题意
有一个无限大的棋盘上有 \(n\) 个互不攻击的车 \((X_i,Y_i)\)。车的攻击范围为所在的行和所在的列。
你可以用一个国王替换某一个车。国王的移动方式为每次向上下左右其中一个方向移动一格。特别地,在攻击车时,移动方式为每次向左上、左下、右上、右下四个方向其中一个方向移动一格。
国王不能进入存在的车的攻击范围内。
对于每个 \(i\),求用国王替换第 \(i\) 个车时,在攻击最多的车的前提下,最少需要的移动步数。
\(n\le 2\times 10^5\)
题解
考虑一个简单的 DP。将车按 \(x\) 坐标排序,国王在攻击的过程中,被攻击的车一定是一个区间。用 \(f[L][R][0/1]\) 表示当前已经攻击掉 \([L,R]\) 这些车,国王在车 \(L\)/车 \(R\) 的位置时,攻击最多的车还需要的最少步数。
转移比较简单,不再展开。
注意到若要攻击的区间 \([l,r]\) 满足,横坐标相邻的车纵坐标也相邻,那么假设起点为 \(s\),攻击的路线一定是 \(s\to l\to r\) 或 \(s\to r\to l\)。可以 \(O(1)\) 计算。
然后我们发现,如果我们将这样的极大区间看成一个整体,我们可以将这个区间继续往左右两边扩张,扩张后的区间仍然存在类似的性质。可以结合下图理解:
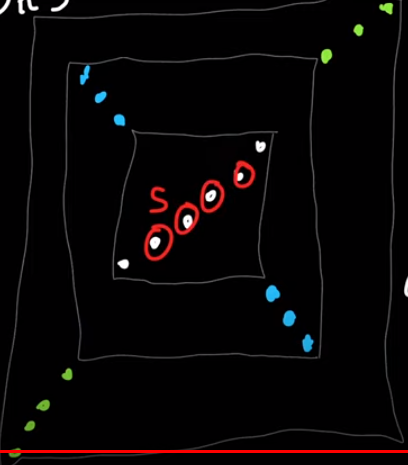
于是我们只要将每次扩张的区间作为 DP 的状态进行 DP 即可。
注意到最开始的区间中的每个点作为起点时,都可以快速计算,于是我们可以通过这样的一次扩张和 DP 将初始的区间中每个车作为起点的答案都计算出来。
结合上图可以发现,只有在扩张白色点时才会将白色、蓝色、绿色的点都访问一遍,而扩张蓝色点、绿色点时都只会扩张出本身的一个区间,所以每个点最多被访问 \(2\) 次。
还有一个小情况如下:
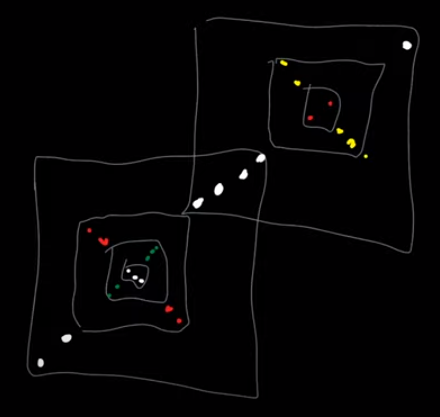
中间的相交部分最多只会被两个大矩形包含,所以最多被访问 \(3\) 次。
最终复杂度瓶颈在于排序和离散的复杂度,扩张和 DP 部分复杂度为线性。
图片来自于官方视频题解。



