「AT1725」「CODE FESTIVAL 2015 OKINAWA OPEN」Cat versus Wolf

AutumnKite

题解AtCoderCODE FESTIVAL 2015 OKINAWA OPEN

发布于：2019年2月12日

次浏览

题目传送门

题意

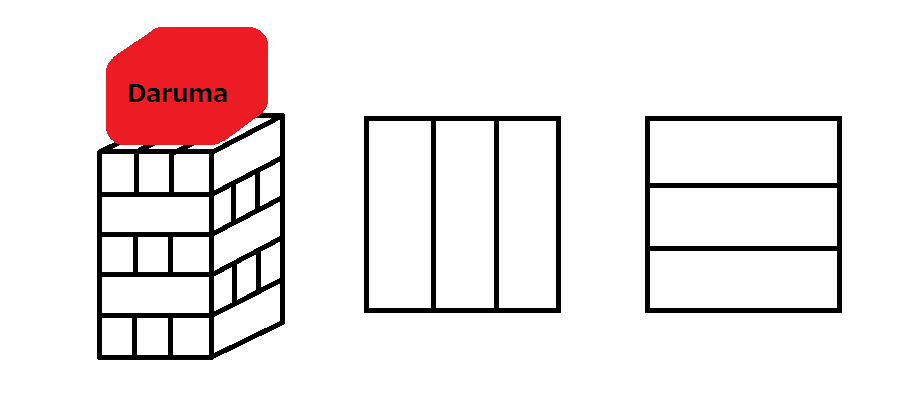
给定一个初始状态如图所示的建筑，共 \(n\) 层（不包括 Daruma），自底向上编号 \(1\sim n\)。

下图分别表示建筑的初始状态、奇数层的放置和偶数层的放置。

Snuke 和 Sothe 轮流进行游戏，Snuke 先手，每次游戏可以拿走建筑中的任意一块砖头，但不允许拿走砖头后建筑变得不平衡。如果不存在砖头可以被拿走，那么该玩家输。

给定一个未结束的游戏，判断两人在绝对聪明的情况下，谁是必胜者（需要根据以拿走的砖块数量确定先手）。

不平衡的定义是，\(n\)层中，存在某层没有砖块，或只有一块砖且这块砖在两侧。

\(n\le 50000\)

题解

显然是个博弈问题。且层与层之间独立，所以可以看作是 \(n\) 个单独的游戏的和。那么我们只要求出每一层的 SG 函数值，然后 xor 起来即可。

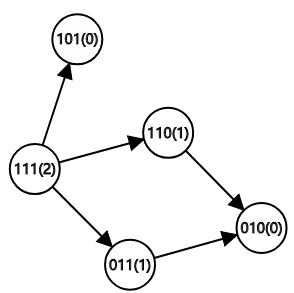
每一层只有 \(2^3-3=5\) 种可能的情况，分类讨论每种情况的 SG 函数值即可。

游戏图如下（0 表示没有砖块，1 表示有砖块，括号内的数表示该状态的 SG 函数值）：

代码

#include <bits/stdc++.h>
int n, S, ans;
char s[3][3];
int main(){
    scanf("%d", &n);
    for (register int i = 1; i <= n; ++i){
        for (register int j = 0; j < 3; ++j) scanf("%s", s[j]);
        if (s[0][0] == '#' && s[1][1] == '#' && s[2][2] == '#') ans ^= 2;
        if (s[0][0] == '.' && s[1][1] == '#' && s[2][2] == '#') ans ^= 1, ++S;
        if (s[0][0] == '#' && s[1][1] == '#' && s[2][2] == '.') ans ^= 1, ++S;
        if (s[0][0] == '.' && s[1][1] == '#' && s[2][2] == '.') S += 2;
        if (s[0][0] == '#' && s[1][1] == '.' && s[2][2] == '#') ++S;
        // 五种情况分类讨论
    }
    printf((!ans) == (S & 1) ? "Snuke\n" : "Sothe\n"); // 注意判断先后手
}

更新于：2021年8月23日

SG函数

「AT1726」「CODE FESTIVAL 2015 OKINAWA OPEN」Dictionary for Shiritori Game

题目传送门题意给定大小为 \(n\) 的字符集和 \(m\) 个单词，第 \(i\) 个单词以字符 \(a_i\) 开头，以字符 \(b_i\) 结尾。 Snuke 和 Sothe 轮...

「AT1724」「CODE FESTIVAL 2015 OKINAWA OPEN」Beware of the Sogginess!

题目传送门题意给定 \(n\) 个二元组 \((a_i,b_i)\)。一个二元组 \((a,b)\) 可以变为 \((a+t,b-t)\ (0\le t\le b)\)。你现在可以选择一...