「AT1729」「CODE FESTIVAL 2015 OKINAWA OPEN」Gorgeous Vases

AutumnKite

题解AtCoderCODE FESTIVAL 2015 OKINAWA OPEN

发布于：2019年2月21日

次浏览

题目传送门

题意

有两个有序二元组 \((A,B),(C,D)\)，\(A,B\) 给定且保证 \(A\ge B\)，\(C,D\) 一开始为 \(0\)。另外给定 \(n\) 个有序二元组 \((p_i,q_i)\)，有两种操作：

\(A\gets A-1,C\gets C+1\)
\(B\gets B-1,D\gets D+1\)

不断执行这两种操作，直到二元组变为 \((0,0),(A',B')\)，其中 \(A',B'\) 表示最初的 \(A,B\)。但任意时刻都需要满足：

\(A\ge B,C\ge D\)
\(\forall i\in [1,n],(A,B)\ne (p_i,q_i),(C,D)\ne (p_i,q_i)\)。

求方案数 \(\bmod (10^9+7)\) 的值。

记操作序列为由每次的操作编号组成的长度为 \(A'+B'\) 的序列，则两个方案不同当且仅当两个方案的操作序列不同。

\(1\le B\le A\le 10^5,0\le n\le 20\)

题解

可以发现，题目可以转化为：

从 \((0,0)\) 走到 \((A,B)\)，每次只能走 \((+1,0)\) 或 \((0,+1)\)（即只能向上、向右走），求满足以下条件的方案数： 1. 对于所有经过的点 \((x,y)\)，\(x\ge y,A-x\ge B-y\) 2. 不能经过点 \((p_i,q_i),(A-p_i,B-q_i)\)。

把 \((A,B)\) 和所有不能经过的点称为障碍点，把障碍点按一定顺序排序后，可以很轻松地写出一个 DP：

\(dp_i\) 表示到达障碍点 \(i\) 的方案数，则 \(dp_i=solve(0,i)-\sum dp_j+solve(j,i)\)，其中 \(j\) 在 \(i\) 的左下方，\(solve(j,i)\) 表示 \(j\) 到 \(i\) 的方案数，\(solve(0,i)\) 表示 \((0,0)\) 到 \(i\) 的方案数。

发现关键在于如何求 \(solve(i,j)\) 的值。那么问题又转化为：

从 \((x_1,y_1)\) 走到 \((x_2,y_2)\)，只能向上、向右走，满足所有经过的点 \((x,y)\) 在直线 \(y=x\) 和 \(y=x-(A-B)\) 之间（包括这两条直线上的点），求方案数。

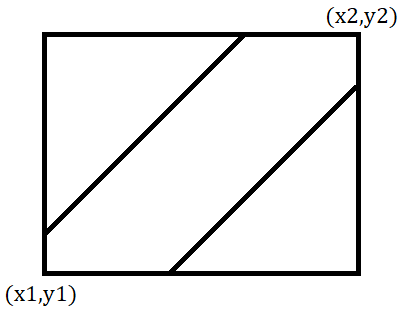
类似上图中的情况，求 \((x_1,y_2)\) 到 \((x_2,y_2)\) 的方案数。

首先，为方便起见，把两条直线分别向上、向下移动一个单位，这样我们就不能碰到这两条直线，碰到即算不符合。

考虑所有情况减去不符合要求的情况，所有情况可以用组合数直接计算，那么我们要计算下图中的两种情况的方案数。

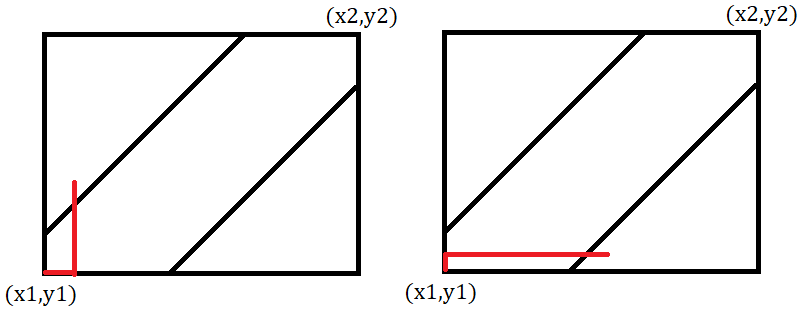
我们先考虑左图的情况，可以发现，左图的情况可以把剩余部分按直线 \(y=x+1\) 对称，如下图所示：

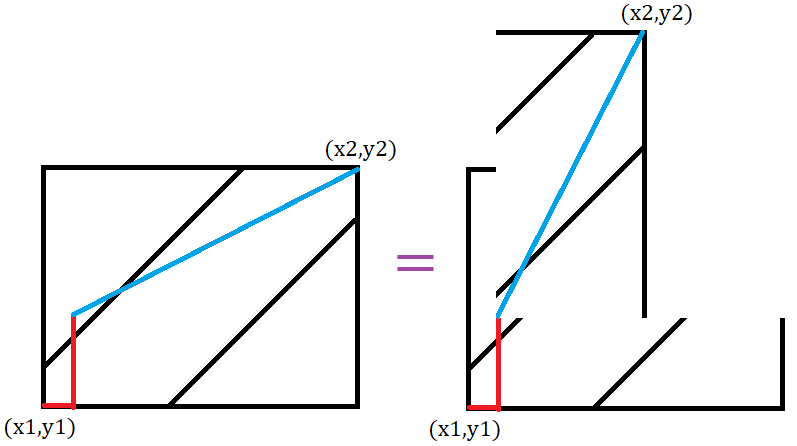
此时 \((x_1,y_1)\) 到 \((x_2,y_2)\) 一定会碰到 \(y=x+1\)，即图 2 中左图的情况。

可是会发现，如果一个方案穿过了 \(y=x+1\)，然后又穿过了 \(y=x-(A-B)-1\)，则这个方案会被重复计算，需要减去。

可以发现，对称后，\(y=x-(A-B)-1\) 这条直线到了最上面，即此时的情况为（下图中的左图）：

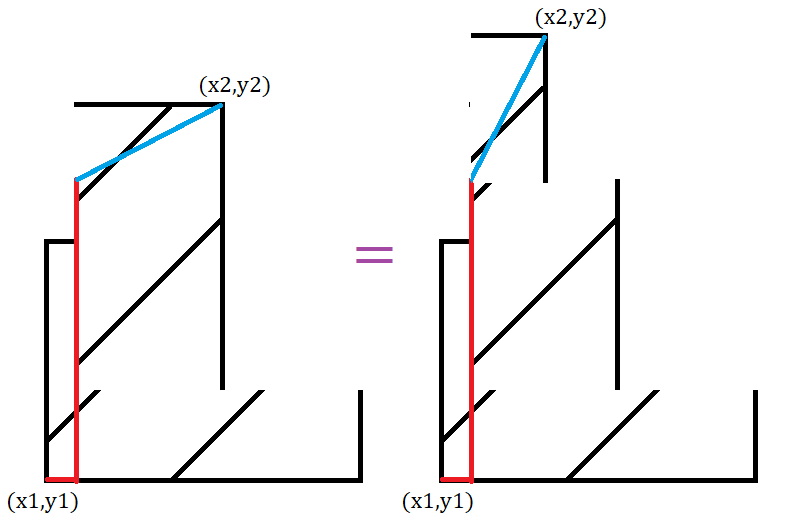
那么同样，对称后计算（如上图右图所示）。

如果还有重复情况（即上下上、上下上下等情况），则继续对称即可。

具体实现及细节见代码。

代码

注意，代码并不是每次作对称然后判断正负的，而是把所有负的都减掉，再把所有正的加上，所以与上面的分析有所出入，请仔细理解。

#include <cstdio>
#include <algorithm>
#define P 1000000007
int A, B, n, m, fac[200005], inv[200005], dp[50];
struct node{
    int x, y;
    bool operator < (const node &res) const {
        return x < res.x || x == res.x && y < res.y;
    }
    bool operator == (const node &res) const {
        return x == res.x && y == res.y;
    }
}p[50];
bool check(int m){
    return p[m].y <= p[m].x && p[m].y >= p[m].x - A + B;
}
int qpow(int a, int b){
    int s = 1;
    for (; b; b >>= 1, a = 1ll * a * a % P) if (b & 1) s = 1ll * s * a % P;
    return s;
}
void pre(int n){
    fac[0] = 1;
    for (register int i = 1; i <= n; ++i) fac[i] = 1ll * fac[i - 1] * i % P;
    inv[n] = qpow(fac[n], P - 2);
    for (register int i = n; i; --i) inv[i - 1] = 1ll * inv[i] * i % P;
}
int F(node a, node b){
    if (a.x > b.x || a.y > b.y) return 0;
    return 1ll * fac[b.x - a.x + b.y - a.y] * inv[b.x - a.x] % P * inv[b.y - a.y] % P;
}
void add(int &x, int y){ (x += y) >= P ? x -= P : 0; }
void del(int &x, int y){ (x -= y) < 0 ? x += P : 0; }
int calc(node a, node b){ // 计算 a 到 b 的方案数，主要难在这个函数
    int res = F(a, b), w = A - B + 2;
    for (register node c = (node){b.y - 1, b.x + 1}; c.x >= a.x; c.x -= w, c.y += w) del(res, F(a, c));
    for (register node c = (node){b.x - w, b.y + w}; c.x >= a.x; c.x -= w, c.y += w) add(res, F(a, c));
    for (register node c = (node){b.y + w - 1, b.x - w + 1}; c.y >= a.y; c.x += w, c.y -= w) del(res, F(a, c));
    for (register node c = (node){b.x + w, b.y - w}; c.y >= a.y; c.x += w, c.y -= w) add(res, F(a, c));
    return res;
}
int main(){
    scanf("%d%d%d", &A, &B, &n), pre(A + B);
    if (A == B) return printf("0\n"), 0;
    for (register int i = 1, x, y; i <= n; ++i){
        scanf("%d%d", &x, &y);
        if (!x && !y) return printf("0\n"), 0;
        if (x == A && x == B) return printf("0\n"), 0;
        p[++m] = (node){x, y}, !check(m) ? --m : 0;
        p[++m] = (node){A - x, B - y}, !check(m) ? --m : 0;
    }
    p[0] = (node){0, 0}, p[++m] = (node){A, B};
    std :: sort(p + 1, p + 1 + m);
    m = std :: unique(p + 1, p + 1 + m) - p - 1;
    for (register int i = 1; i <= m; ++i){
        dp[i] = calc(p[0], p[i]);
        for (register int j = 1; j < i; ++j)
            (dp[i] -= 1ll * dp[j] * calc(p[j], p[i]) % P) < 0 ? dp[i] += P : 0;
    }
    printf("%d\n", dp[m]);
}

更新于：2021年8月23日

数学

组合数学

容斥

「AT1730」「CODE FESTIVAL 2015 OKINAWA OPEN」Happy 2015

题目传送门题意给定 \(n\) 个区间 \((l_r,r_i]\)（注意原题中虽然写着 \([l_i,r_i]\)，但通过转化后相当于 \((l_i,r_i]\)），每个区间有存在和不存...

「AT1728」「CODE FESTIVAL 2015 OKINAWA OPEN」Falconry

题目传送门题意给定平面上 \(n\) 个点 \((x_i,y_i)\)，以及三只鸟的初始坐标 \((x_a,y_a),(x_b,y_b),(x_c,y_c)\)。现在三只鸟要从初始点开始...