「AT1735」「Xmas Contest 2015」Colored Tiles

AutumnKite

题解AtCoderXmas Contest 2015

发布于：2019年5月18日

次浏览

题目传送门

题意

这是一道交互题。

交互库中生成了一个 \(n\times m\) 的每个格子有颜色的矩阵。颜色可以有任意多种。给定的是 \(n,m\)。记矩阵中第 \(x\) 行第 \(y\) 列的颜色为 \(col(x,y)\)（矩阵的行列下标从 \(1\) 开始）。

你可以进行询问，询问的格式是 ? x1 y1 x2 y2，交互库会告诉你 \(col(x1,y1)=col(x2,y2)\) 并且 \(col(x1,y2)=col(x2,y1)\) 是否成立。询问次数不能超过 \(4\,500\)。

最后你应该输出 ! ans，\(ans\) 表示中心对称的子矩阵的数量。

\(n\le 5,m\le 100\)

题解

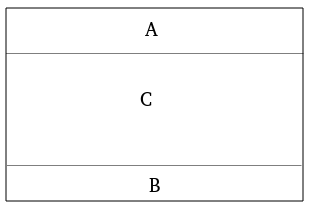
上图这个矩阵如果是中心对称的，那么 \(A\) 反转一下一定与 \(B\) 相等，且 \(C\) 也是中心对称的。

那么考虑 \(A,B\) 两行，设他们的行号分别为 \(i,j\)，中间位置为 \(k\)，两边为 \(l,r\)，那么 \(A\) 反转一下与 \(B\) 相等可以转化成 \(\forall 0\le x\le k-l,col(i,k-x)=col(j,k+x)\text{ and }col(i,k+x)=col(j,k-x)\)。这个与询问的格式就一样了。

并且可以发现，这是一个“类回文”的形式，所以可以用 manacher 解决，这样就可以减少询问次数。为了解决奇偶性问题，可以当作把每行扩展一倍，在相邻两个格子之间插入其他字符，注意询问时候要变回原来的下标。

就是说，对于任意两行 \(i,j(1\le i\le j\le n)\)，求出每列向左右可以扩展的最多的列数。然后枚举矩阵的上下两行和对称中心所在的列数，求出在该条件下的极大中心对称的矩阵的列数，然后直接统计。

可以用 map 减少一定量的询问次数。

代码

#include <cstdio>
#include <algorithm>
#include <map>
int n, m, len[6][6][205];
struct node{
    int a, b, c, d;
    bool operator < (const node &res) const {
        return a < res.a || (a == res.a && b < res.b) || (a == res.a && b == res.b && c < res.c) || (a == res.a && b == res.b && c == res.c && d < res.d);
    }
};
std :: map<node, int> M;
bool check(int x1, int y1, int x2, int y2){
    if (x1 > x2 || y1 > y2 || x1 < 1 || x2 > n || y1 < 1 || y2 > (m >> 1)) return 0;
    if (x1 == x2 && y1 == y2) return 1;
    if (M.count((node){x1, y1, x2, y2})) return M[(node){x1, y1, x2, y2}];
    printf("? %d %d %d %d\n", x1, y1, x2, y2), fflush(stdout);
    char opt[5];
    scanf("%s", opt);
    return M[(node){x1, y1, x2, y2}] = (opt[0] == 'y');
}
void manacher(int x, int y, int *hw){
    int mr = 0, mid = 0, n = m;
    hw[0] = 1;
    for (register int i = 1; i <= n; ++i){
        hw[i] = i <= mr ? std :: min(hw[(mid << 1) - i], mr - i + 1) : 0;
        if (i + hw[i] <= mr) continue;
        while ((i - hw[i]) % 2 == 0 || check(x, (i - hw[i] + 1) / 2, y, (i + hw[i] + 1) / 2)) ++hw[i];
        if (i + hw[i] - 1 > mr) mid = i, mr = i + hw[i] - 1;
    }
}
int main(){
    scanf("%d%d", &n, &m);
    m <<= 1;
    for (register int i = 1; i <= n; ++i)
        for (register int j = i; j <= n; ++j)
            manacher(i, j, len[i][j]);
    int ans = 0;
    for (register int i = 1; i <= n; ++i)
        for (register int j = i; j <= n; ++j)
            for (register int k = 1; k <= m; ++k){
                int s = 1e9;
                for (register int l = i, r = j; l <= r; ++l, --r)
                    s = std :: min(s, len[l][r][k]);
                ans += s >> 1;
            }
    printf("! %d\n", ans), fflush(stdout);
}

更新于：2021年8月23日

交互

manacher

「AT1736」「Xmas Contest 2015」Destroy the Duplicated Poem

题目传送门题意有 \(n+1\) 个字符串 \(S_0,S_1,S_2,\cdots,S_n\)。\(S_0\) 是空串，\(S_i\) 是 \(S_{a_i}\) 后加上字符 \(c_...

「Codeforces 1156E」Special Segments of Permutation

题目传送门题意给定一个长度为 \(n\) 的排列 \(a\)，求有多少区间 \([l,r]\) 满足 \(a_l+a_r=\max\limits_{i=l}^{r}a_i\)。 \(n...