A - Consecutive Integers
题意
求在 \(1\) 到 \(N\) 的整数中选择连续的 \(K\) 个整数的方案数。
\(N\le 50\)
题解
显然答案为 \(N-K+1\)。
B - RGB Boxes
题意
求有多少非负整数三元组 \((r,g,b)\) 满足 \[Rr+Gg+Bb=N\]
\(N\le 3000\)
题解
枚举其中两个即可。
时间复杂度 \(O(N^2)\)。
C - AB Substrings
题意
给定 \(N\) 个字符串 \(s_i\),将这些字符串按任意顺序拼接,求 AB 作为子串的出现次数的最大值。
\(N\le 10^4,|s_i|\le 10\)
题解
先将每个字符串中间的 AB 计入贡献,那么剩余的字符串可以分为 xxx、xxA、Bxx、BxA 四种。
那么一定是用所有 BxA 和至多一个 xxA 和 Bxx 拼出 xxABxABxA...BxABxx 这样的字符串,再用剩下的 xxA 和 Bxx 拼 xxABxx 这样的字符串。
注意细节。
D - DivRem Number
题意
给定正整数 \(N\),求有多少正整数 \(m\) 满足 \(\lfloor\frac{N}{m}\rfloor=N\bmod m\)。
\(N\le 10^{12}\)
题解
化一下式子,得到 \(\lfloor\frac{N}{m}\rfloor(m+1)=N\)。那么 \(m+1\) 一定是 \(N\) 的因数,枚举即可。
时间复杂度 \(O(\sqrt{N})\)。
E - XOR Partitioning
题意
给定序列 \(A_1,A_2,\ldots,A_N\),将该序列划分成若干段,使得每段的异或和相等,求方案数。对 \(10^9+7\) 取模。
\(N\le 5\times 10^5\)
题解
对原序列作前缀和 \(S_i\),假设每段的异或和为 \(x\),那么一个合法的划分方案一定是选择 \(S\) 中一个 \(x\) 和 \(0\) 交替的子序列。
考虑枚举 \(x\),然后 DP。令 \(f_i\) 表示前 \(i\) 个数,强制 \(i\) 选择且 \(S_i=x\) 时合法方案数。那么有 \[f_i=1+\sum_{j=0}^{i-1} f_j(c_i-c_j)\]
其中 \(c_i\) 表示 \(S_1,S_2,\ldots,S_i\) 中 \(0\) 的数量。
最终答案与段数的奇偶性有关,段数为奇数时为 \(f_N\),段数为偶数时为所有 \(f_i\) 的和。段数的奇偶性可以通过 \(S_N\) 是否等于 \(0\) 确定。
用前缀和优化 DP 转移,时间复杂度 \(O(N)\)。注意特判 \(x=0\) 的情况。
F - Edge Ordering
题意
给定一个 \(N\) 个点 \(M\) 条边的简单无向连通图 \(G\),保证前 \(N-1\) 条边构成了 \(G\) 的一个生成树。
你需要给每条边确定一个 \(1\) 到 \(M\) 的整数边权,需要保证边权互不相同。
对于一个确定边权的方案,我们称该方案是好的当且仅当前 \(N-1\) 条边构成的生成树是最小生成树。
求所有好的方案的最小生成树边权和之和。对 \(10^9+7\) 取模。
\(N\le 20\)
题解
假设原图如下图(重绘自官方题解):
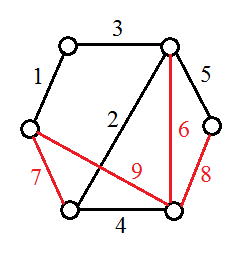
其中边上的数字为边的编号,黑边为树边,红边为非树边。
我们假设前 \(N-1\) 条边的边权按 \(1\) 到 \(N-1\) 的顺序递增,例如上图中有 \(cost(1) < cost(2) < \ldots < cost(5)\)。为了使这五条边成为最小生成树,我们需要保证其余非树边 \((u,v)\) 的边权需要大于树上 \(u\) 到 \(v\) 路径上最大的边权。例如图中 \(cost(7) > cost(3),cost(9) > cost(4)\)。
我们可以根据边权的大小关系建出一个拓扑关系图,例如上图对应的拓扑图如下图所示(来自官方题解):
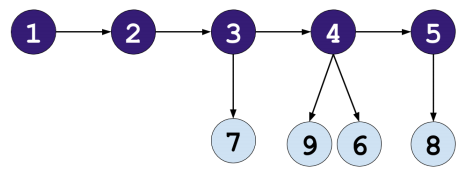
令 \(a_i\ (1\le i\le N-1)\) 表示上图中 \(i\) 向下的连边数量,即点 \(i\) 向编号大于 \(N-1\) 的点的连边数量。
那么我们可以把问题转化为,有 \(M\) 个有标号的球,你有一个空的序列 \(S\),球会按 \(a_{N-1}\) 个白球,一个黑球,\(a_{N-2}\) 个白球,一个黑球……这样的顺序给你,例如上图对应的球的序列为 \(8,5,9,6,4,7,3,2,1\)。每收到一个球,你可以执行以下操作:
- 若收到的球是黑球,则在 \(S\) 的最前面插入该球。
- 若收到的球是白球,则插入到 \(S\) 的任意位置。
求最终得到的所有 \(S\) 序列中黑球的位置编号和之和。
考虑在依次收到球的过程中,维护 \(n\) 表示当前序列 \(S\) 的长度,\(b\) 表示 \(S\) 中黑球的数量,\(c\) 表示不同的序列 \(S\) 的数量,\(s\) 表示所有序列 \(S\) 中黑球的位置编号之和的和。用 \((n,b,c,s)\) 表示当前的状态。
若收到一个黑球,那么新的状态为 \((n+1,b+1,c,s+(b+1)c)\)。
若收到一个白球,假设原来的序列中黑球的位置为 \(p_1,p_2,\ldots,p_b\),不妨假设 \(p_0=0,p_{b+1}=n+1\),那么插入该白球时的总变化量(即每个位置的贡献之和)为 \[ \sum_{i=1}^{b+1}(p_i-p_{i-1})(b-i+1)=\sum_{i=1}^{b}p_i \]
所以新的状态为 \((n+1,b,(n+1)c,(n+1)s+s)\),即 \((n+1,b,(n+1)c,(n+2)s)\)。
那么加入 \(k\) 个白球后新的状态为 \((n+k,b,\frac{(n+k)!}{n!}c,\frac{(n+k+1)!}{(n+1)!}s)\)。
对于原来的问题,我们并没有固定前 \(N-1\) 条边边权的大小关系,所以需要 DP。考虑到上面的问题是按边权从大到小进行转移的,那么这里的 DP 也从大到小确定边权的大小关系。
令 \(f_S=(n,b,c,s)\),\(S\) 表示该集合中边权的大小关系仍未确定,不在该集合中的边的边权都大于在该集合中的边的边权。\(n,b,c,s\) 的定义与之前类似。转移只需要枚举下一条边,\(c,s\) 的转移与上面问题类似。
实现精细可以做到 \(O(2^NN)\)。



