题目传送门

题意

有 $n$ 棵树，第 $i$ 棵树高度为 $a_i$。你需要砍掉一些树，砍树规则如下：

1. 只能砍最多 $m$ 棵树。
2. 对于每个 $i\ (1\le i\le n-k+1)$，满足 $[i,i+k-1]$ 中被砍掉的树的数量不超过 $1$。

被砍掉的树的位置的高度都变为 $0$。

求砍树后 $\max\limits_{1\le i\le n-k+1}\sum\limits_{j=i}^{i+k-1} a_j$ 的最小值，即最小化所有长度为 $k$ 的区间的树的高度之和的最大值。

$n\le 10^5,a_i\le 10^9$

题目传送门

题意

有 $n$ 天，每天有一个值 $a_i$（未确定的值），其中 $a_i=0$ 的天数称为“休息”，其他的称为“工作”。

若第 $i$ 天为“工作”，设第 $i$ 天之前（不包含第 $i$ 天）连续“工作”的天数为 $k$，则 $a_i=\max(0,A-kB)$（$A,B$ 给定）；若第 $i$ 天为“休息”，则 $a_i=0$。

现已经确定 $m$ 天为“休息”，求 $\sum_{i=1}^{n} a_i$ 的最大值。

$n,A,B\le 10^9,m\le 10^5$

题目传送门

题意

给定 $n$ 个区间 $(l_r,r_i]$（注意原题中虽然写着 $[l_i,r_i]$，但通过转化后相当于 $(l_i,r_i]$），每个区间有存在和不存在两种状态。求所有 $2^n$ 种方案中，本质不同的方案的数量 $\bmod (10^9+7)$ 的值。

记一个方案的点集合为数轴上至少被一个区间覆盖的整数组成的集合，则两个方案本质不同当且仅当这两个方案的点集合不同。

$n\le 2000,0\le l_i< r_i\le 10^9$

题目传送门

题意

有两个有序二元组 $(A,B),(C,D)$，$A,B$ 给定且保证 $A\ge B$，$C,D$ 一开始为 $0$。另外给定 $n$ 个有序二元组 $(p_i,q_i)$，有两种操作：

1. $A\gets A-1,C\gets C+1$
2. $B\gets B-1,D\gets D+1$

不断执行这两种操作，直到二元组变为 $(0,0),(A',B')$，其中 $A',B'$ 表示最初的 $A,B$。但任意时刻都需要满足：

1. $A\ge B,C\ge D$
2. $\forall i\in [1,n],(A,B)\ne (p_i,q_i),(C,D)\ne (p_i,q_i)$。

求方案数 $\bmod (10^9+7)$ 的值。

记操作序列为由每次的操作编号组成的长度为 $A'+B'$ 的序列，则两个方案不同当且仅当两个方案的操作序列不同。

$1\le B\le A\le 10^5,0\le n\le 20$

题目传送门

题意

给定平面上 $n$ 个点 $(x_i,y_i)$，以及三只鸟的初始坐标 $(x_a,y_a),(x_b,y_b),(x_c,y_c)$。现在三只鸟要从初始点开始，依次飞到一些点（不需要回到起点），要求每个点至少被一只鸟飞到。求三只鸟总飞行距离之和的最小值。

从一个点 $(x_s,y_s)$ 飞到另一个点 $(x_t,y_t)$ 的飞行距离为这两个点的欧几里得距离，即 $\sqrt{(x_s - x_t)^2 + (y_s - y_t)^2}$

$n\le 18$，所有横纵坐标的绝对值 $\le 10^4$，时限 $8s$。

题目传送门

题意

$H\times W$ 的矩阵，第 $i(0\le i< H)$ 行第 $j(0\le j< W)$ 列的数为 $iW+j$。

选一个子矩阵，使得该子矩阵中所有元素 xor 的值最大。输出这个值。

$H,W\le 10^9$

题目传送门

题意

给定大小为 $n$ 的字符集和 $m$ 个单词，第 $i$ 个单词以字符 $a_i$ 开头，以字符 $b_i$ 结尾。

Snuke 和 Sothe 轮流玩单词接龙游戏（Snuke 先手）。每次游戏那个人必须说出一个以上个单词的末尾字符开头的单词，第一个人必须说出一个以字符 1 开头的单词。若轮到该人进行游戏时，说不出符合条件的单词，则该人失败。

假设两人绝对聪明，判断谁是胜者或者游戏会永远进行下去。

$n\le 10^5,m\le 2\times 10^5$

题目传送门

题意

给定一个初始状态如图所示的建筑，共 $n$ 层（不包括 Daruma），自底向上编号 $1\sim n$。

下图分别表示建筑的初始状态、奇数层的放置和偶数层的放置。

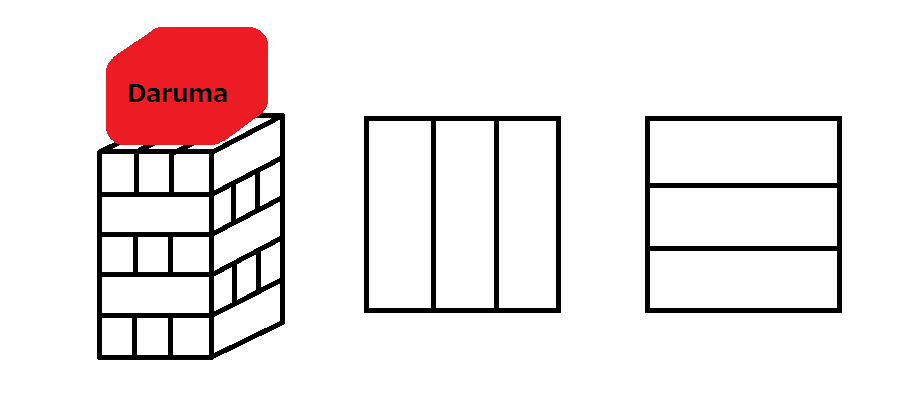
Snuke 和 Sothe 轮流进行游戏，Snuke 先手，每次游戏可以拿走建筑中的任意一块砖头，但不允许拿走砖头后建筑变得不平衡。如果不存在砖头可以被拿走，那么该玩家输。

给定一个未结束的游戏，判断两人在绝对聪明的情况下，谁是必胜者（需要根据以拿走的砖块数量确定先手）。

不平衡的定义是，$n$层中，存在某层没有砖块，或只有一块砖且这块砖在两侧。

$n\le 50000$

题目传送门

题意

给定 $n$ 个二元组 $(a_i,b_i)$。一个二元组 $(a,b)$ 可以变为 $(a+t,b-t)\ (0\le t\le b)$。你现在可以选择一些二元组并将它们分别进行（即互相独立）一次变换，使得变换后你选择的所有二元组 $(a_j,b_j)$，$\sum a_j\ge A,\sum b_j\ge B$。求最少需要选择并变换的二元组数量。

$1\le n\le 50,1\le A,B,a_i,b_i\le 10^4$

题目传送门

题意

构造一张 $H\times W$ 的由岛屿#、海洋.组成的地图，岛屿为八连通，满足恰好包含 $K$ 个联通块。

$1\le H,W\le 100,1\le K\le 10000$